超簡単 体積の求め方 苦手な数学を簡単に
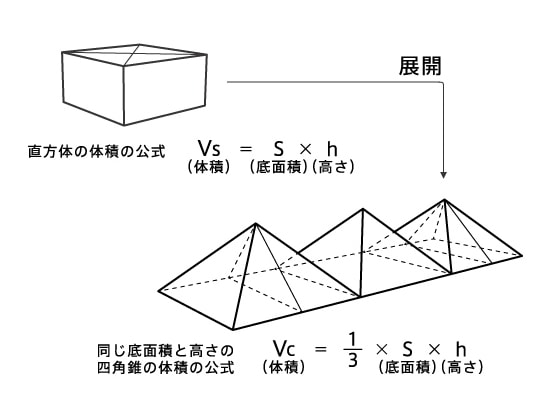
三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介します。四角錐台 五角錐台 円錐台 の面積が0)とすると錐体の体積の公式、s = s (上底と下底の面積が等しい)とすると柱体の体積の公式になる。 この項目は、初等幾何学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています 最終更新 21年8月6日 (金)
四角錐の体積 公式
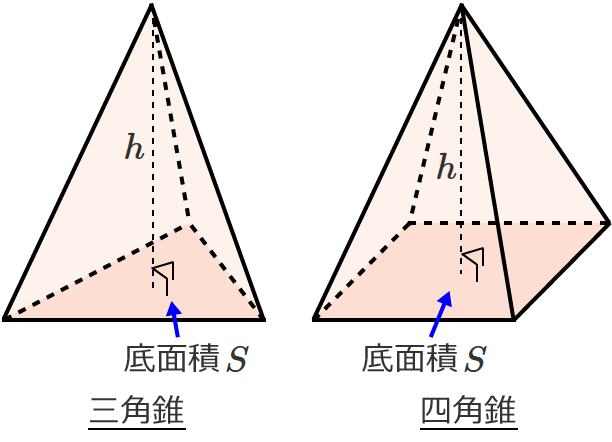
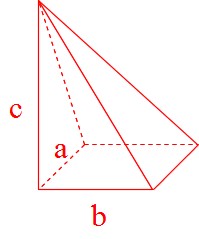
四角錐の体積 公式-角錐の体積の公式は? 角錐の体積の公式は 底面積×高さ×3分の1(又は、底面積×高さ÷3) です。角錐は底面が多角形の錐体です。三角錐、四角錘、円錐など色々な形状がありますが、体積の公式は全て同じです。 下図の三角錐の体積を算定しましょう。底面は三角形なので三角形の面積=底辺×高さ÷2です。あとは高さを掛けて3で割ればよいのです。正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積
三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
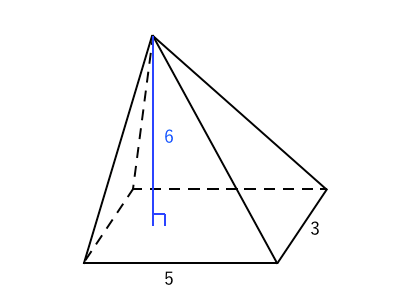
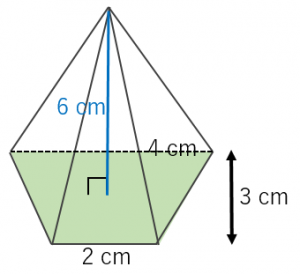
角錐の高さと体積 解説 次の図のようなすべての辺の長さがaの正三角錐(正四面体)abcdについて考えます。 頂点aから底面bcdに垂線ahを引くと,このahの長さが正四面体の高さになります。このとき,図のように abhに着目すると直角三角形であるので,三平方の定理を利用してahの長さを四角すいの体積 A: B: H: 体積: 球 球 半球 中空球 円周から体積 円柱 円柱 パイプ 円周から体積 立方体 立方体・直方体 角パイプ 錐体 円すい 四角すい 多角形 6錘体の体積は、柱体の1/3で算定できます。底面の台形の上底長さ3、下底長さ5、高さが4、四角錘の高さ6のとき、 四角錐の体積=(35)÷2×4×6÷3=32cm 3 です。 角錐の体積の公式は?1分でわかる公式、柱体の体積との違い、3分の1になる証明 三角錐の体積
$$\large{四角錐の体積=底面積\times高さ\color{red}{\times \frac{1}{3}}}$$ 四角錐の体積を求めるときに気をつけたいのは、 必ず\(\frac{1}{3}\)を掛ける ことです。 さて、全く同じ形の四角錐6つが立方体に綺麗に収まっていますね。 したがって四角錐1つの体積は、 a 3 ×1/6 となります。 ⑤ 公式を作ろう。 では次は公式化してみましょう。 今考えていた四角錐の底面は1辺がaの正方形なので、底面積は、 a×a=a 2 ですね。角錐・円錐の体積の求め方には底面積×高さ÷3という公式があります。 「なぜ、÷3するのか」という疑問を解決するために、四角錐などの立体を組み合わせて考えました。 自分たちが体積を求められる立体になるように、くっつけ方を考え、「÷3」の理由を導き出しました。 6年担任 與座 幹太
四角錐の体積 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 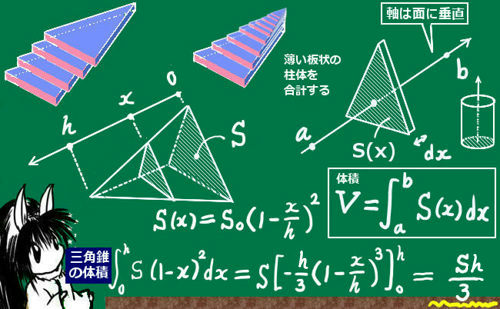 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
「四角錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 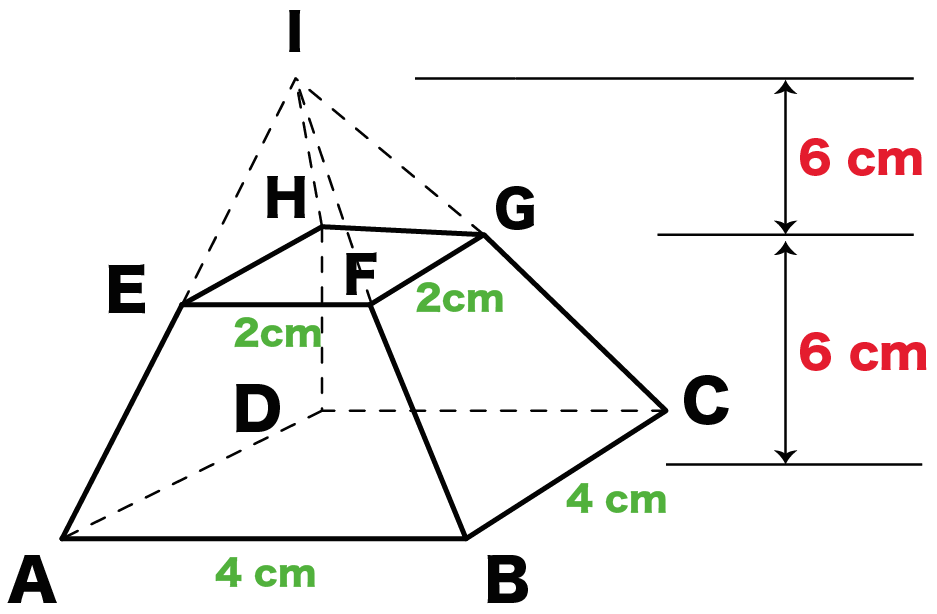 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 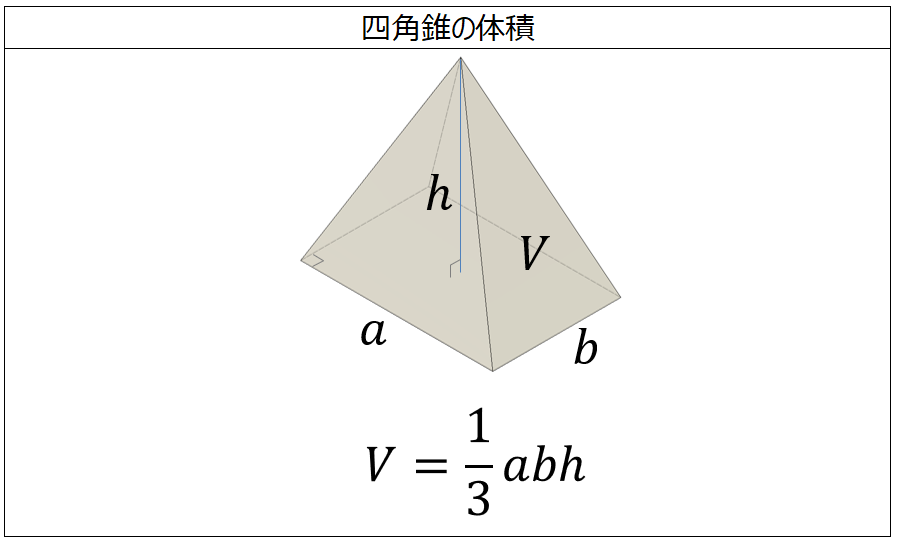 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
「四角錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
「四角錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
「四角錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
「四角錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
「四角錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
「四角錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 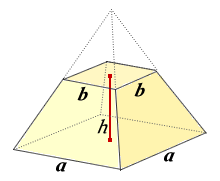 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
「四角錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 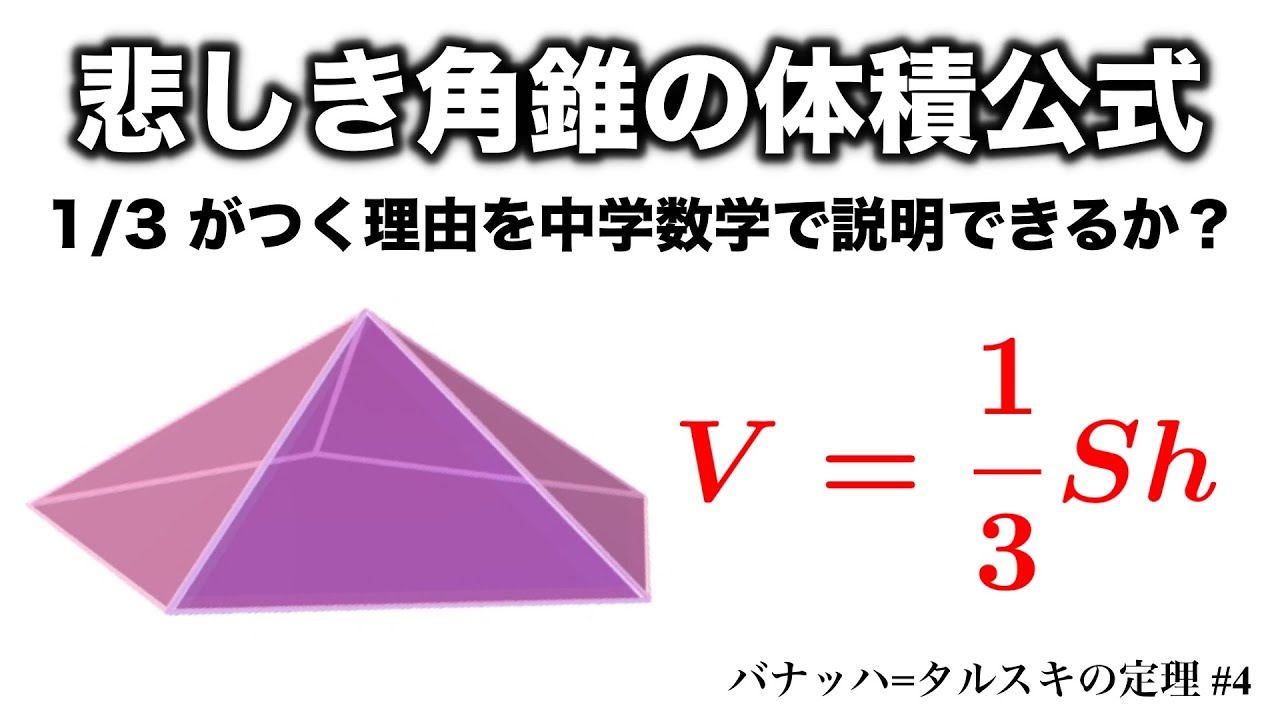 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
「四角錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 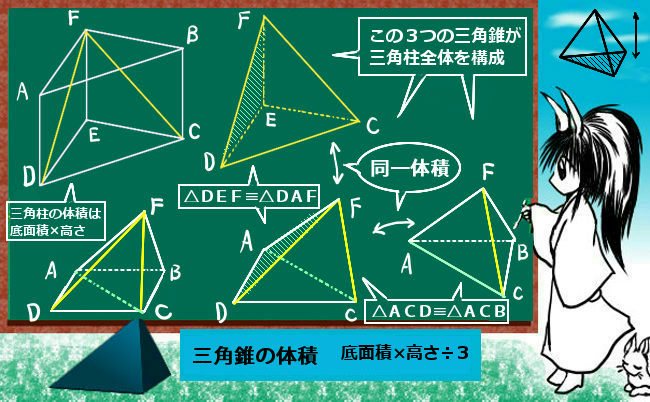 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 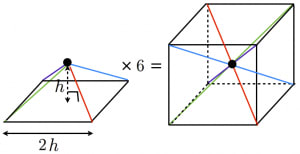 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
「四角錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
「四角錐の体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 | 四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |  四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後 |
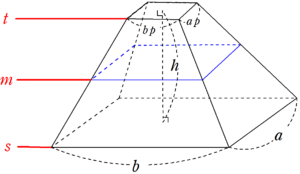
三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 立体は切断したり、展開したりしてできる限り平面で考える 直方 よって、シンプソンの公式で体積は次のように計算できる。 \begin{equation} \displaystyle \frac{ts}{6} \left\{ f(s) 4f(m) f(t) \right\}
Incoming Term: 四角錐の体積 公式,




0 件のコメント:
コメントを投稿